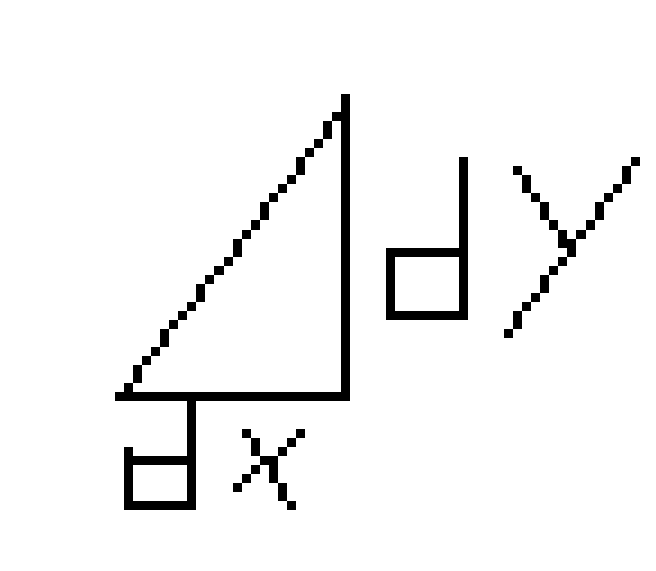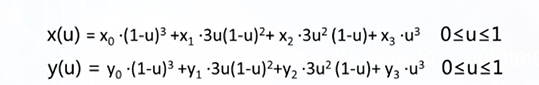第一部分软光栅

(1)绘制线段

1 思路

image-20201114003525837

如上图所示，当画一条线时，首先计算增量dx，dy。如果dy<dx，则x方向增长快，每次必加1，而y看判别式。

取dx所在线（x轴平行线）和画的线所成角的角平分线，若新的y落在该平分线上面，则y递增，否则y不变。而角平分线方程为：$dy=\frac{1}{2}dx$，即平分斜率。即$dy-\frac{1}{2}dx>0 \Longrightarrow 2dy-dx>0$时，y递增。此时下一个判别式的增量为$2(dy-dx)$。否则增量为$2dy$。

为了将直线扩展到所有斜率使用，实现使用了动态增量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
function drawLine(p1, p2){
	var x1 = p1[0], y1 = p1[1];
	var x2 = p2[0], y2 = p2[1];
	/// 下方代码用以绘制线段

    //由(x1,y1)画到(x2,y2)，设置绘制起始点
	var x = x1;
	var y = y1;
    //计算差值
	var dx = x2 - x1;      
	var dy = y2 - y1;
    //计算增量。如dx小于0，则x每次递增都是减1，反之加1.y同理
	var ix = (dx > 0) ? 1 : -1;
	var iy = (dy > 0) ? 1 : -1;
	dx = Math.abs(dx);
	dy = Math.abs(dy);
    //如果x比y增长的快
	if(dx > dy)
	{
        //初始化判别式
		var p = 2 * dy - dx;
		for(var i = 0; i <= dx; i++)
		{
			addPixel(x,y);
            //x增长的快，x每次都递增
			x += ix;
            //如果判别式大于0，y递增，p更新
			if(p >= 0)
			{
				y += iy;
				p += 2 * (dy - dx);
			}
			else
			{
				p += 2 * dy;
			}
		}
	}
    //y增长快的情况，x和y互换即可
	else
	{
		var p = 2 * dx - dy;
		for(var i = 0; i <= dy; i++)
		{
			addPixel(x,y);
			y += iy;
			if(p >= 0)
			{
				x += ix;
				p += 2 * (dx - dy);
			}
			else
			{
				p += 2 * dx;
			}
		}
	}
	
	/// 上方代码用以绘制线段
}
2重点难点

（1）实现全斜率直线绘制

（2）DDA浮点数远算到Bresenham整数远算的优化过程思考

3心得

掌握了DDA的基本思想和由其升级得到的Bresenman算法。

(2)画圆

1 思路

根据圆心在原点的圆的方程$R^2=x^2+y^2$和圆的性质得：$F(x,y)=x^2+y^2-R^2$。

选取第二象限0-45度得圆弧作为绘制得基本圆弧，其他七个区域有基本圆弧对称得出。

在基本圆弧中，x得初始值为0，y得初始值为R。由于基本圆弧中，x的变化率大于y，令x每一步都递增1，而y由判别式判断是否递增。

考虑当前点$P(x,y)$,下一步递增有两个候选点$P_b(x+1,y-1)$,$P_u(x+1,y)$。选取候选点的方式是判断两点的中点$P_m(x+1,y-0.5)$是落在园内还是圆外。若落在圆内，说明$P_u$距离圆弧更接近，选择$P_u$，否则选择$P_b$。

而判断方式由函数$F(x,y)$判定。$F(x,y)<=0则在院圆内或圆上,F(x,y)>0则在圆外$。

若当前$F(x,y)<=0$，则当前的$F_{current}(x,y)=(x+1)^2+(y-0.5)^2-R^2$，下一个$F_{next}(x,y)=(x+1+1)^2+(y-0.5)^2-R^2$。所以得到判别式的差值$\Delta d=F_{next}(x,y)-F_{current}(x,y)=2x+3$。

若当前$F(x,y)>0$，则当前的$F_{current}(x,y)=(x+1)^2+(y-0.5)^2-R^2$，下一个$F_{next}(x,y)=(x+1+1)^2+(y-0.5-1)^2-R^2$。所以得到判别式的差值$\Delta d=F_{next}(x,y)-F_{current}(x,y)=2(x-y)+5$。

而判别式的初值$d_0=F(1,\frac{R+(R-1)}{2})=1.25-R$。

然后对判别式进行浮点数优化。由于判别式的差值为整数，所以$d_0=D_0-0.25=1-R$。而$0.25 \in (0,1)$，直接舍去。

这样就计算出了基本圆弧的每一个点。然后对基本圆弧的点以圆心$(cx,cy)$进行八个方向对称：$(cx \pm x,cy \pm y),(cx \pm y,cy \pm x)$。画出圆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
let d = 1-radius;//初始化差值
let y = radius;//初始化y
let xMax = radius/Math.sqrt(2);//计算x的右边界
//x开始增量迭代
for(let x = 0;x<=xMax;++x){
	
       //8次调用对应八个方向对称
	addPixel(centerx+x,centery+y);
	addPixel(centerx+x,centery-y);
	addPixel(centerx-x,centery+y);
	addPixel(centerx-x,centery-y);
	
	addPixel(centerx+y,centery+x);
	addPixel(centerx+y,centery-x);
	addPixel(centerx-y,centery+x);
	addPixel(centerx-y,centery-x);
	//判别式更新，x递增在for循环里
	if(d<=0){
		d += 2*x+3;
	}
	else{
		d += 2*(x-y)+5;
		--y;
	}
	
}
2重点难点

（1）浮点数优化。

（2）判别式去浮点数的推导。

3心得

（1）对浮点数优化成整数运算有了一些启蒙性的感悟。

（2）明白了最终代码都是算法精简后的结果，研究算法时要先实现完整过程在优化。否则不知道那一步出错或中间过程不具有可调试性。降低效率。

（3）实践理解了Bressenham中点画圆法及其优化。

(3)绘制多边形

1 思路

（1）建立边表ET

将每一个边加入边表，获取y的最大最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function initEdgeTable(points){
	let ET = {};
	let yMin = 1000000000;
	let yMax = 0;
	for(var index = 0;index<points.length - 1;++index){
		let result = addToET(points[index],points[index + 1],ET);//加入边表
		ET = result.ET;
	
		yMin = Math.min(yMin,result.yMin);
		yMax = Math.max(yMax,result.yMax);
	}
	
	let result = addToET(points[0],points[points.length - 1],ET);
	ET = result.ET;
	
	yMin = Math.min(yMin,result.yMin);
	yMax = Math.max(yMax,result.yMax);
	
	return {ET: ET, yMin: yMin, yMax: yMax};
}

一条边加入边表的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function addToET(point1,point2,ET){
    //另point1始终未y较小的点
	if(point2[Loc.Y] < point1[Loc.Y])
		[point1,point2] = [point2,point1];
    //构造边节点，ivK为增量
	let edge = {
		x: point1[Loc.X],
		yMax: point2[Loc.Y],
		ivK: (point2[Loc.X]-point1[Loc.X])/(point2[Loc.Y] - point1[Loc.Y]),
	};
		
	if(ET[point1[Loc.Y]] == undefined){
		ET[point1[Loc.Y]] = [];
	}
	
	ET[point1[Loc.Y]].push(edge);
	
	return {ET: ET, yMin: point1[Loc.Y], yMax: point2[Loc.Y]};
}

（2）开始迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
	let AET = [];
//从最小的y开始到最大的y
	for(let currentY = result.yMin;currentY<=result.yMax;++currentY){
        //遍历活动边表的所有边
		for(let index = 0;index < AET.length;++index){
            //如果扫描线已经在边的上面，把边删去
			if(currentY > AET[index].yMax){
				AET.splice(index,1);
				--index;
			}
            //否则这条边的x坐标增加一个增量
			else{
				AET[index].x += AET[index].ivK;
			}
		}
		//查看当前扫描线是否扫描到新的边
		let edges = ET[currentY];
		if(edges != undefined){
            //将新的边加入边表
			for(let index = 0;index < edges.length;++index){
				AET.push(edges[index]);
			}
		}
		
        //将互动边表根据x坐标排序，若x相等则更具增量排序
		AET.sort(function(left,right){
			if(left.x == right.x) return left.ivK - right.ivK;
			return left.x - right.x;
		});
		let isDraw = false;
        //遍历活动边表开始填充
		for(let index = 0;index < AET.length - 1;++index){
            //交替填充
			isDraw = !isDraw;
			if(!isDraw)continue;
			drawLine(
			[AET[index].x,currentY],
			[AET[index + 1].x,currentY]
			);
		}
	}
2重点难点

边表数据结构的建立

3心得

（1）实践了js的许多语法和debug手段，加强了js编码能力。

（2）学会了js实现链表，哈希表数据结构。

（3）实践理解了有序边表法。理解了先前有些疑惑的地方。

（4）绘制贝塞尔曲线

1 思路

通过三次贝塞尔多项式：image-20201114001026575

对0到1进行采样计算出多个点的函数值，然后连接起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function drawCurve(p1, p2, p3, p4){
    //确定路径起点
	let lineP = [p1,];
    //在0到1中进行采样
    for (let dt=0;dt<=1;dt+=0.001)
    {
        //计算函数值
        let yt=1-dt;
		let c1=yt*yt;
		let c2=3*yt*dt;
		let dt3 = dt*dt*dt;
        let xt=p1[0]*c1*yt+p2[0]*c2*yt+p3[0]*c2*dt+p4[0]*dt3;
        yt=p1[1]*yt*c1+p2[1]*c2*yt+p3[1]*c2*dt+p4[1]*dt3;
        //将当前点加入路径
		lineP.push([xt,yt]);
    }
	//一次绘制这些路径
	for(let index = 0;index < lineP.length - 1;++index){
		drawLine(lineP[index],lineP[index+1]);
	}
}
2重点难点

（1）贝塞尔曲线公式的展开和推到

（2）采样率的选择

3心得

（1）了解了不同采样率选取对绘图的影响，这是一个性能和效果的权衡。不过就本题的例子而言，，最高的效果性能也远远足够。

（2）加深了对贝塞尔曲线的理解和使用

第二部分 gasket分形

1 思路

image-20201114001405923

如上图所示，每一次分型实际上就是绘制四个三角形。三个彩色一个白色。每个三角形有三个顶点。只要确定着12个顶点的位置和颜色即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//p1,p2,p3为大三角形的三个顶点
function recurse(p1,p2,p3,depth){
    //深度为0返回
    if(depth==0){
        return;
    }
    //分别计算三个顶点的中点
    let mid12 = [(p1[0]+p2[0])/2,(p1[1]+p2[1])/2];
    let mid23 = [(p2[0]+p3[0])/2,(p2[1]+p3[1])/2];
    let mid13 = [(p1[0]+p3[0])/2,(p1[1]+p3[1])/2];
    //为这4个三角形12个顶点指定坐标和颜色
    //p1,mid12,mid13为左下角三角形三个点
    //mid12,p2,mid23为上方角三角形三个点
    //mid13,mid23,p3为右下角三角形三个点
    //mid12,mid23,mid13为中间白色三角形三个点
    triangles.push(p1,mid12,mid13,mid12,p2,mid23,mid13,mid23,p3,mid12,mid23,mid13);
    //分别指定颜色
    triangleColors.push(red,green,blue,red,green,blue,red,green,blue,white,white,white);
	//分别将外围三个彩色三角形作为大三角形继续递归
    recurse(p1,mid12,mid13,depth-1);
    recurse(mid12,p2,mid23,depth-1);
    recurse(mid13,mid23,p3,depth-1);
}
2重点难点

（1）递归算法设计

（2）代码精简和可读性维护

3心得

（1）加强了自己递归算法的设计能力

（2）学会了webgl颜色的设置

（3）实践了分形几何的自相似性的递归实现。自相似性本身就是递归的特性。