学习笔记——最小生成树
@[toc]
简介
规定点的数量为V,边为E
生成树是指在连通图中包含所有节点的一棵树,即该树包含所有节点的同时每个节点的入度出度均为1。而一幅图的生成树有很多种,其中最小生成树指的是带权图的生成树中边权和最小的树。并且若图中的边权都不相同,则最小生成树唯一(每两个节点都只有一条边相连,每次选最小的),反之,就不一定了。
最小生成树一般有两个通用的算法,一个是Prim算法,一个是Kruskal算法。
Prim算法
Prim算法被形象的描述为一棵小树逐渐长大。首先,先从图中任意选取一个节点,寻找离该节点最近的节点合并形成一棵树,再更新各个相连节点到该树的距离,再找最小,合并直到长成节点树为V的树,即为最小生成树。
那在向树添加节点的过程中,怎样更新各节点到树的距离呢?首先,我们可以先定义一个优先队列(一种每次key值最大/最小的元素都在队首的数据结构),每次取结点时,将该节点所有邻接节点都丢入队列(未直接相连的先不管,因为只要是和树未直接相连的节点距离一定小于直接相连的),然后每次从队首中取出一个(距离最子树小的)节点,再更新直到树上有V个节点任务就完成了。
时间复杂度
若采用邻接链表存图,优先队列(一种二叉堆)每次插入都需要$log{2}V$次操作,而一共入队$V$次所以时间复杂度为$O(Vlog{2}V)$
Q1最短网络
原题传送门_>洛谷P1546
整个网络就是一张图,光纤的最小长度就是最小生成树的边权和。
1 |
|
Kruskal算法
除了Prime算法1,还有Kruskal可以求最小生成树。Kruskal算法是一种贪心思想,首先先将边权排序,将边权最小的边的两个节点放入同一个集合,然后看第二小的边,如果改边的两个点再同一集合内,就跳过改边,否则就继续,直到合并了$V-1$条边。这里点的集合操作采用并查集的方式。
还是以Q1作为例子1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
using namespace std;
struct Edge {
int from, to, val;//边类,包含两个节点和权重
};
struct twice {
int p, w;
};
vector<Edge> edge;//边集
int n;
//并查集
int f[10001];
int find(int x) {
if (x == f[x]) return x;
f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> n;
int x;
for (int i = 1; i <= n; i++)
{
f[i] = i;
for (int j = 1; j <= n; j++)
{
cin >> x;
if (i != j)
{
edge.push_back({ i,j,x });
}
}
}
sort(edge .begin(), edge .end(), [](Edge&l, Edge&r)//边权排序
{
return l.val < r.val;
});
int ans = 0, cnt = 0;
for (int i = 0; i < edge.size(); i++)//从小到大
{
if (find(edge[i].from) == find(edge[i].to))continue; //如果在同一集合
//内就continue
ans += edge[i].val;//答案更新
f[find(edge[i].from)] = edge[i].to;//将两个点加入同一集合
cnt++;//边数加一
if (cnt == n - 1) break;//边数达到n-1就退出
}
cout << ans;
return 0;
}
时间复杂度
并查集每次操作复杂度$log{2}V$,一共循环E次,而排序E条边时$O(Elog{2}E)$,所以复杂度$O(Elog_{2}E)$
二者取舍
因为Prim算法以点为单位,所以适合对付稠密图,而Kruskal算法对付稀疏图。
Q2公路修建
原题传送门->洛谷P1265
条件(1)保证了图里没有重边
条件(2)每次选路都只会选最近的城市修路,如果真有环,比如题设A离B最近,B离C最近,C离A最近,这不可能,除非有虫洞 可以手动模拟。
那就变成每次各个城市都选最近的城市修路,合并,修路,合并,而且每两个城市都只有一条路相连,着不就是Prime的实现过程。所以,这里我采用了Prime。滑稽.jpg
首先暴力存图,算出各个城市的距离,然后存图,然后收获了可爱的MLE
60分code
1 |
|
以上代码和上一道题操作一样,没啥好说的。
既然空间暴了,那咋办呢,我们发现,看了某dalao提示,距离只有距离更新和选节点时才用到,所以Kruskal死了 ,只要入队时再计算距离即可。毕竟5000的数据$O(n^{2})$的时间复杂度完全过得了,就不用堆了。
ACcode
1 |
|
Q3 Slim Span(苗条生成树)
题意简述
求所有生成树中最大边权与最小边权差最小的,输出它们的差值。
输入:
输入文件包含多组测试数据,每组测试数据如下: 第1行:2个整数n m (2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2),n表示顶点数,m表示边数。接下来m行,每行3个空格分开的整数a b w(1 ≤ w ≤ 10000) , 表示顶点a与顶点b之间有一条边,权值为w。
输出:
对每组测试数据,如果图存在生成树,输出生成树的差值最小的;否则,输出-1。
将边权排序,一共有$|E|$条边,设排好序的边集合为$A={e1,e_2,\cdots ,e{|E|} }$,那对于任意的$i,j,1\leq i \leq j \leq |E|$,对于$A$的子集合$S{ij}={e_i,e{i+1},\cdots ,ej}$,$S{i,j}$若能生成原图的生成树,则由$S_{i,j}$所生成的最小生成树的苗条度$\leq {e_j-e_i}$。所以将$i,j$做一个全排列,枚举每一对$i,j$组合即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
using namespace std;
int n, m;
constexpr int inf = 2000000000;
//边
struct Edge {
int from, to, val;
explicit Edge(int& f, int& t, int& v) :from(f), to(t), val(v) { }
bool operator<(const Edge& Right)const noexcept {
return val < Right.val;
}
};
//并查集
struct DisSet {
int Father[101];
//初始化
void init(const int& n)noexcept {
for (int i = 1; i <= n; ++i) {
this->Father[i] = i;
}
}
int find(int x)noexcept {
int& F = Father[x];
return x == F ? x : (F = find(F));
}
//合并
void merge(const Edge&edge)noexcept {
this->Father[this->find(edge.from)] = this->find(edge.to);
}
//判断是否同一集合
bool query(const Edge& edge)noexcept {
return this->find(edge.from) == this->find(edge.to);
}
}DSet;
vector<Edge> Edges;
inline void input() {
Edges.clear();
for (int i = 0; i < m; ++i) {
int from, to, val;
scanf("%d%d%d", &from, &to, &val);
Edges.emplace_back(from, to, val);
}
}
inline int getAns() {
int Ans = inf;
for (int i = 0; i < m; ++i) {
DSet.init(n);
int cnt = 0;
for (int j = i; j < m; ++j) {
const Edge& Cur = Edges[j];
if (!DSet.query(Cur)) {
DSet.merge(Cur);
++cnt;
if (cnt == n - 1) {
Ans = min(Ans, Edges[j].val - Edges[i].val);
break;
}
}
}
}
return Ans == inf ? -1 : Ans;
}
int main() {
while (true) {
scanf("%d%d", &n, &m);
if (!m && !n)break;
input();
sort(Edges.begin(), Edges.end());
printf("%d\n", getAns());
}
}
时间复杂度:$O(m^2)$
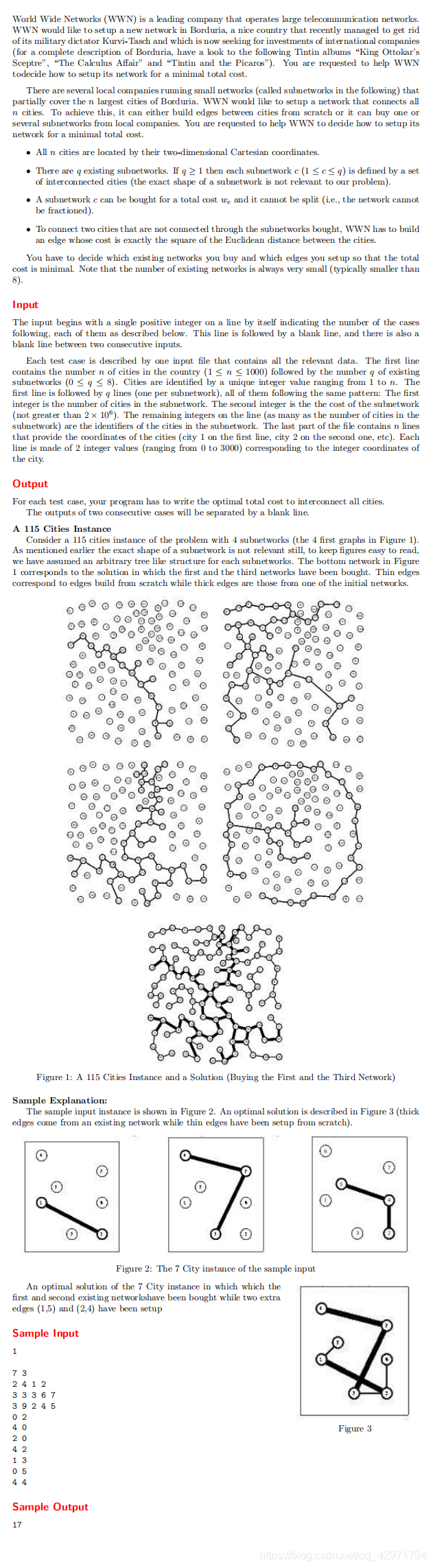
Q4 Buy or Build
题目描述
万维网(WWN)是一家运营大型电信网络的领先公司。 WWN希望在Borduria建立一个新的网络,您需要帮助WWN确定如何以最低的总成本设置其网络。有几个本地公司运营着一些小型网络(以下称为子网),部分覆盖了Borduria的n个最大城市。 WWN希望建立一个连接所有n个城市的网络。 要实现这一目标,它可以从头开始在城市之间建设网络,也可以从本地公司购买一个或多个子网。 您需要帮助WWN决定如何以最低的总成本建设其网络。
1、所有n个城市都给出其二维坐标
2、存在q个子网。 如果$q≥1$,给出每个子网中连接的城市。(不用关心连接的形状)
3、每个子网只能购买,不能被分割
4、连接两个不相通的城市,必须建立一个边,其建设成本是城市之间欧几里德距离的平方。
您的任务是决定购买哪些现有网络以及建设哪些边,使得总成本最低。
输入格式
输入文件的第一行是一个整数T,表示测试数据的组数。接下来是一个空白行。每两组测试数据之间也有一个空白行。
对于每组测试数据:
第一行是两个整数,分别是城市的总数n和子网的数量q,1≤n≤1000,0≤q≤8。城/市的编号从1到n
接下来q行,每行多个整数,第一个整数表示这个子网中的城市的数量m,第二个整数表示购买这个子网的费用(费用不超过$2*10^6$),剩下的m个整数表示这个子网包含的城市
接下来n行,每行两个整数,表示第i个城市的坐标(坐标的数字范围是0到3000)
输出格式
对于每组测试数据输出一行,输出建设网络的总费用。每组输出之间用一个空行隔开
Translated by @kevensice__
引用自洛谷
不购买子网络的情况,只要求相应的最小生成树就好了,记此时的最小生成树对应的边集合为$A$。而对于购买子网络的情况,显然此时的最优解中的边要么出现在子网络中,要么出现在$A$中。当我们购买子网络时,先将子网络中的边加入并查集,然后再在A中找边来生成最小生成树即可。(采用Kruskal算法)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
using namespace std;
int n, t;
constexpr int inf = 2000000000;
//点
struct Node {
int x, y, node;
explicit Node(int& x, int& y,int&node) :x(x), y(y),node(node) { }
int getSquare(const int& x)const {
return x * x;
}
int getDis(const Node& Right)const {
return getSquare(x - Right.x) + getSquare(y - Right.y);
}
};
//边
struct Edge {
int from, to;
int dis;
explicit Edge(const Node&Left, const Node& Right) {
from = Left.node;
to = Right.node;
dis = Left.getDis(Right);
}
explicit Edge() = default;
bool operator<(const Edge& Right)const noexcept {
return dis < Right.dis;
}
};
//子网络
struct NetWork {
int N, Cost;
vector<int> Has;
void input() {
scanf("%d%d", &N, &Cost);
for (int i = 1; i <= N; ++i) {
int point;
scanf("%d", &point);
Has.push_back(point);
}
}
};
//并查集
struct DisSet {
int Father[1001];
void init(const int& n)noexcept {
for (int i = 1; i <= n; ++i) {
this->Father[i] = i;
}
}
int find(int x)noexcept {
int& F = Father[x];
return x == F ? x : (F = find(F));
}
void merge(const Edge&edge)noexcept {
this->Father[this->find(edge.from)] = this->find(edge.to);
}
void merge(const NetWork& network) {
const auto& points = network.Has;
if (points.size() < 2) {
return;
}
const int& F = this->find(points.front());
for (int i = 1; i < points.size(); ++i) {
this->Father[this->find(points[i])] = this->find(F);
}
}
bool query(const Edge& edge)noexcept {
return this->find(edge.from) == this->find(edge.to);
}
}DSet;
vector<Edge> Edges;
vector<Node> nodes;
vector<NetWork> networks;
inline void input() {
networks.clear();
nodes.clear();
networks.resize(t);
for (int i = 0; i < t; ++i) {
networks[i].input();
}
for (int i = 1; i <= n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
nodes.emplace_back(x, y, i);
}
}
//将点装欢为边,没两点之间都生成一条边
inline void getEdge() {
Edges.clear();
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
Edges.emplace_back(nodes[i], nodes[j]);
}
}
}
//计算最小生成树
inline int getMST() {
vector<Edge>temp;//用来保存最小生成树
int&& cnt = 0;
int&& Ans = 0;
DSet.init(n);
sort(Edges.begin(), Edges.end());
for (const auto& edge : Edges) {
if (!DSet.query(edge)) {
DSet.merge(edge);
++cnt;
Ans += edge.dis;
temp.push_back(edge);
if (cnt == n - 1) {
Edges = temp;//此时Edges为最小生成树
return Ans;
}
}
}
}
//计算最小生成树
inline int Transver(vector<Edge>& Edges) {
int&& Ans = 0;
for (const auto& edge : Edges) {
if (!DSet.query(edge)) {
DSet.merge(edge);
Ans += edge.dis;
}
}
return Ans;
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &t);
input();
getEdge();
int&& Ans = getMST();
//采用位运算枚举所有子网络的购买方式
for (int i = 1; i <= (1 << t) - 1; ++i) {
DSet.init(n);
int&& Cost = 0;
for (int cnt = 0, j = i; j; j >>= 1, ++cnt) {
if (j & 1) {
const NetWork& Cur = networks[cnt];
DSet.merge(Cur);
Cost += Cur.Cost;
}
}
Ans = min(Ans, Cost + Transver(Edges));
}
printf("%d\n", Ans);
if (T) {
putchar('\n');
}
}
return 0;
}
时间复杂度:$O(2^q(n^2logn))$
Q5:
Q5 Qin Shi Huang’s National Road System
题目pdf
题目链接
题目大意: n个城市,需要修建一些道路使得任意两个城市联通,还可以修一条魔法道路, 不花钱, 设魔法路连接的城市的人口之和为A, 所有道路总长为B, 求A/B的最大值。
可以先求一遍最小生成树,然后枚举每一对点,求若将这两个点作为魔法道路的最小生成树,然后不断更新答案即可。
举个例子:
假如有${1,2,3,4,5}$,5个节点组成了下图的最小生成树。1
2
3
4
5graph LR
1((1))---2((2))
1((1))---3((3))
3---4((4))
3---5((5))
假如在4,5之间修建魔法道路,那么此时会变成:1
2
3
4
5
6graph LR
1((1))---2((2))
1((1))---3((3))
3---4((4))
4--0---5((5))
3---5((5))
此时3,4,5形成了一个环。显然4,5之间的边权重为0,而此时要想重新形成最小生成树,就需要在环中去掉一条边,那自然是去掉权重最大的边了。由于新加的边权重为0,所以最大边只能出先在原最小生成树上。对于任意节点$i,j$,在最小生成树上只有唯一的互通路径,而最大边只能出现在路径上。因此,用最大边替换魔法道路得到的权值和是最小的,此时($B=$原最小生成树权重和$-$最大边)。因此,先求出最小生成树后,在树上DFS求出任意两点间路径的最大边,在枚举每一对点即可。
而若$i,j$在最小生成树上直接相连,例如在3,5之间修建魔法道路,会形成如图:
1
2
3
4
5graph LR
1((1))---2((2))
1((1))---3((3))
3---4((4))
3--0---5((5))
此时3,5之间的最大边唯一,将此边换成魔法道路,(B=原最小生成树权重和$-$最大边)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
using namespace std;
int n;
//节点
struct Node {
int x, y, P, node;
Node(int& x, int& y, int& P,int&node) :x(x), y(y), P(P),node(node) { }
double getSquare(const double& x)const {
return x * x;
}
double getDis(const Node& Right)const {
return sqrt(
getSquare(x - Right.x) +
getSquare(y - Right.y)
);
}
};
//边
struct Edge {
int from, to;
double dis;
Edge(const Node& Left, const Node& Right) :from(Left.node), to(Right.node), dis(Left.getDis(Right)) { }
bool operator<(const Edge& Right)const {
return dis < Right.dis;
}
};
//并查集
struct {
int Father[1001];
void init() {
for (int i = 1; i <= 1000; ++i) {
this->Father[i] = i;
}
}
int find(int x) {
int& F = this->Father[x];
return x == F ? x : (F = this->find(F));
}
void merge(const Edge& edge) {
this->Father[this->find(edge.from)] = this->find(edge.to);
}
bool query(const Edge& edge) {
return this->find(edge.from) == this->find(edge.to);
}
}DSet;
vector<Node>nodes;
vector<Edge> edges;
void input() {
scanf("%d", &n);
nodes.clear();
for (int i = 1; i <= n; ++i) {
int x, y, P, node;
scanf("%d%d%d", &x, &y, &P);
nodes.emplace_back(x, y, P, i);
}
}
//将点转换为边
void initEdge() {
edges.clear();
for (int i = 0; i < nodes.size(); ++i) {
for (int j = i + 1; j < nodes.size(); ++j) {
edges.emplace_back(nodes[i], nodes[j]);
}
}
}
//计算最小生成树
double getMST() {
vector<Edge>temp;
DSet.init();
stable_sort(edges.begin(), edges.end());
int&& cnt = 0;
double&& Ans = 0;
for (const Edge& edge : edges) {
if (!DSet.query(edge)) {
DSet.merge(edge);
++cnt;
temp.push_back(edge);
Ans += edge.dis;
if (cnt == n - 1) {
edges = temp;
return Ans;
}
}
}
return Ans;
}
double Dis[1001][1001];//Dis[i][j]为i到j在最小生成树上的最大边
bool Vis[1001];
struct Point {
int node;
double dis;
Point(const int& cur,const double& dis) :node(cur), dis(dis) { }
Point() = default;
};
vector<Point>G[1001];
//DFS计算Dis
void getDis() {
//G为邻接链表
for (int i = 1; i <= n; ++i) {
G[i].clear();
Vis[i] = false;
}
//建表
for (const Edge& edge : edges) {
G[edge.from].emplace_back(edge.to,edge.dis);
G[edge.to].emplace_back(edge.from, edge.dis);
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
Dis[i][j] = 0.;
}
}
//DFS
for (int i = 1; i <= n; ++i) {
stack<Point> S;
S.emplace(i,0.);
for (int i = 1; i <= n; ++i) {
Vis[i] = false;
}
while (!S.empty()) {
Point cur = S.top();
S.pop();
if (Vis[cur.node])continue;
Vis[cur.node] = true;
Dis[i][cur.node] = max(Dis[i][cur.node], cur.dis);
Dis[cur.node][i] = max(Dis[cur.node][i], cur.dis);
for (const Point& Next : G[cur.node]) {
S.emplace(Next.node,max(cur.dis,Next.dis));
}
}
}
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
input();
initEdge();
double&& W = getMST();
getDis();
double&& Ans = 0.;
//枚举计算最大的A/B
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
Ans = max(Ans, static_cast<double>(nodes[i].P + nodes[j].P) / (W-Dis[nodes[i].node][nodes[j].node]));
}
}
printf("%.2lf\n", Ans);
}
return 0;
}
时间复杂度:$O(n^2)$
Q6 Edges in MST
题目描述
You are given a connected weighted undirected graph without any loops and multiple edges.Let us remind you that a graph’s spanning tree is defined as an acyclic connected subgraph of the given graph that includes all of the graph’s vertexes. The weight of a tree is defined as the sum of weights of the edges that the given tree contains. The minimum spanning tree (MST) of a graph is defined as the graph’s spanning tree having the minimum possible weight. For any connected graph obviously exists the minimum spanning tree, but in the general case, a graph’s minimum spanning tree is not unique.Your task is to determine the following for each edge of the given graph: whether it is either included in any MST, or included at least in one MST, or not included in any MST.
输入格式
The first line contains two integers n and m ( $2\leq n\leq 10^5$ , ) — the number of the graph’s vertexes and edges, correspondingly. Then follow m m m lines, each of them contains three integers — the description of the graph’s edges as “ $a{i}b{i}w{i}$ “ ( $1\leq a_i,b_i\leq n,1\leq w_i\leq 10^6,ai≠bi$ ), where $a{i}$ and $b{i}$ are the numbers of vertexes connected by the$i{th}$ edge, $w{i}$ is the edge’s weight. It is guaranteed that the graph is connected and doesn’t contain loops or multiple edges.输出格式Print m m m lines — the answers for all edges. If the $i{th}$ edge is included in any MST, print “any”; if the $i{th}$ edge is included at least in one MST, print “at least one”; if the $i{th}$ edge isn’t included in any MST, print “none”. Print the answers for the edges in the order in which the edges are specified in the input.
题目大意:
给一个带权的无向图,保证没有自环和重边. 由于最小生成树不唯一,因此你需要确定每一条边是以下三种情况哪一个 :
1.一定在所有MST上
2.可能在某个MST上
3.一定不可能在任何MST上
输入第一行给出n,m表示点数和边数. 数据范围见原题面 之后m行,每行给出ai,bi,wi 表示一个边的两个端点和边的权值.保证没有自环与重边. 输出你需要输出m行,每行依次表示输入的第几条边,如果是情况1,输出 “any”(不包含引号);如果是情况2,输出 “at least one”(不包含引号);如果是情况3,输出 “none”(不包含引号).
输入输出样例
输入
4 5
1 2 101
1 3 100
2 3 2
2 4 2
3 4 1
输出
none
any
at least one
at least one
any
输入
3 3
1 2 1
2 3 1
1 3 2
输出
any
any
none
输入
3 3
1 2 1
2 3 1
1 3 1
输出
at least one
at least one
at least one
说明/提示
In the second sample the MST is unique for the given graph: it contains two first edges.In the third sample any two edges form the MST for the given graph. That means that each edge is included at least in one MST.
对于某条边,如果它权值大于最小生成树上的相应边,那就是none,如果它等于相应边并且是桥边,那就是any,不是桥边那就是at least one了。Tarjan找桥。
1 |
|
Q7 ACM Contest and Blackout
题目pdf
题目链接
题目要求非严格次小生成树。
次小生成树和最小生成树一定只有一条边不同,即将最小生成树的其中一条边替换掉。
和Q5类似,先求最小生成树,再遍历所有不在最小生树中的边,将其替换即可。
1 |
|
时间复杂度:$O(n^2logn)$
Q8 Arctic Network
The Department of National Defence (DND) wishes to connect several northern outposts by a wireless network. Two different communication technologies are to be used in establishing the network: every outpost will have a radio transceiver and some outposts will in addition have a satellite channel.
Any two outposts with a satellite channel can communicate via the satellite, regardless of their location. Otherwise, two outposts can communicate by radio only if the distance between them does not exceed D, which depends of the power of the transceivers. Higher power yields higher D but costs more. Due to purchasing and maintenance considerations, the transceivers at the outposts must be identical; that is, the value of D is the same for every pair of outposts.
Your job is to determine the minimum D required for the transceivers. There must be at least one communication path (direct or indirect) between every pair of outposts.
Input
The first line of input contains N, the number of test cases. The first line of each test case contains 1 <= S <= 100, the number of satellite channels, and S < P <= 500, the number of outposts. P lines follow, giving the (x,y) coordinates of each outpost in km (coordinates are integers between 0 and 10,000).
Output
For each case, output should consist of a single line giving the minimum D required to connect the network. Output should be specified to 2 decimal points.
Sample Input
1
2 4
0 100
0 300
0 600
150 750
Sample Output
212.13
题目大意:
给出一张图,求该图的最小瓶颈生成树。
瓶颈生成树:
无向图$G$的一颗瓶颈生成树是这样的一颗生成树:它最大的边权值在$G$的所有生成树中是最小的。瓶颈生成树的值为T中最大权值边的权。
该图建立在坐标系中, 给出每个点的坐标。任意两点之间都有边,边权即为两点间的距离。
瓶颈生成树就是最小生成树,因为在树中每两个点之间只有一条边,所以最小生成树就是选择两点间最短的边,而瓶颈生成树同样也是取最小边。
1 |
|
时间复杂度:$O(n^2logn)$
Q9 Conquer a New Region
题目大意:
有N个城镇(编号从1到N),由几条公路连接起来。任何两个城镇之间都有一条确切的路线。我们定义道路的容量C(i,j),表示允许最多C(i,j)货物在镇i和镇j之间运输。如果镇 i 和 镇 j 之间有道路连通的话,我们定义了一个值S(i,j),它表示i和j之间唯一通路上容量的最小值。我们的国王想要选择一个中心城市来恢复他的战争资源。使中心到其他 N−1 个城镇交通能力(即到其他所有点的容量之和)最大化。现在,你,这个王国里最好的程序员,应该能帮助我们的国王选择这个中心。
简述:
假设 N (N <= 200000) 个城市形成一棵树,每条边有权值 C(i,j)。任意两个点的容量 S (i ,j)定义为 i 与 j 唯一通路上容量的最小值。找一个点(它将成为中心城市),使得它到其他所有点的容量之和最大。
输入:
有多个测试样例。
每一种情况下第一行一个整数 N (1 ≤ N ≤ 200, 000)
之后 N-1 行 每行包含三个整数 A , B , C ,表明 A 城和 B 城之间有一条容量为 C 的道路。 (1 ≤ a, b ≤ N, 1 ≤ c ≤ 100, 000)
输出:
对于每个测试用例,输出一个整数,表示所选择的中心城镇的总交通容量。
翻译来自洛谷
在树中,每一条边都是桥边。
假设对于生成树${1,2,3,4,5,6}$,设集合$A={1,2,3}$,集合$B={4,5,6}$,此时要将$A,B$合并。记$F(x)$为以$x$作为中心的总容量。1
2
3
4
5graph LR
1((1))---3((3))
2((2))---3((3))
4((4))---5((5))
4---6((6))
可以看到,若将$A,B$合并,则A中的点到B必定经过$E{34}$,B同理。若$E{34}$比$A,B$中的权值都小,那么(合并后的$F(A)=$合并前的$F(A)+B$中点的数量$E{34}$的权值)。$B$同理。1
2
3
4
5
6graph LR
1((1))---3((3))
2((2))---3((3))
3--E_34---4((4))
4---5((5))
4---6((6))
所以为了保证$E{34}$是最小的,在合并生成树前,我们将边按从大到小排序。然后在比较$A,B$哪个作为中心容量和更大,哪个就作为生成树的父节点,即作为中心城市。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
using namespace std;
int n;
struct Node {
int x, y, P, node;
Node(int& x, int& y, int& P,int&node) :x(x), y(y), P(P),node(node) { }
constexpr double getSquare(const double& x)const {
return x * x;
}
double getDis(const Node& Right)const {
return sqrt(
getSquare(x - Right.x) +
getSquare(y - Right.y)
);
}
};
struct Edge {
int from, to;
int dis;
Edge(int& from, int& to, int& dis) :from(from), to(to), dis(dis) { }
bool operator<(const Edge& Right)const {
return dis > Right.dis;
}
};
struct {
int Father[200001];
void init(const int&n) {
for (int i = 1; i <= n; ++i) {
this->Father[i] = i;
}
}
int find(int x) {
int& F = this->Father[x];
return x == F ? x : (F = this->find(F));
}
void merge(const Edge& edge) {
this->Father[this->find(edge.from)] = this->find(edge.to);
}
bool query(const Edge& edge) {
return this->find(edge.from) == this->find(edge.to);
}
}DSet;
vector<Node>nodes;
vector<Edge> edges;
int Ans[200001],//Ans[i]表示当前以i点为中心的容量和
Cnt[200001];//Cnt[i]表示i点所在的集合的点的数量
void input() {
edges.clear();
for (int i = 1; i <= n-1; ++i) {
int from, to, val;
scanf("%lld%lld%lld", &from, &to, &val);
edges.emplace_back(from, to, val);
Ans[i] = 0;
Cnt[i] = 1;
}
Cnt[n] = 1;
Ans[n] = 0;
}
signed main() {
while (~scanf("%lld", &n)) {
input();
stable_sort(edges.begin(), edges.end());
DSet.init(n);
for (const Edge& edge : edges) {
int fx = DSet.find(edge.from);
int fy = DSet.find(edge.to);
//容量和大的作为中心,作为父节点
if (fx != fy){
if (Ans[fy] + Cnt[fx] * edge.dis > Ans[fx] + Cnt[fy] * edge.dis) {
swap(fx, fy);
}
Ans[fx] += Cnt[fy] * edge.dis;
DSet.Father[fy] = fx;
Cnt[fx] += Cnt[fy];
}
}
printf("%lld\n", Ans[DSet.find(1)]);
}
return 0;
}
*时间复杂度:$O(n^2logn)$
Q10 Bond
题目pdf
题目链接
题目大意:求两点间最短路中的最大边。
用Kruskal算法求最小生成树(并查集不要路径压缩,保留树结构),然后遍历两点间的树上唯一路径找最大边即可。
1 |
|
时间复杂度:$O(N^2logN+QlogN)$