学习向量 Learning Vector

UVA12589
预处理：
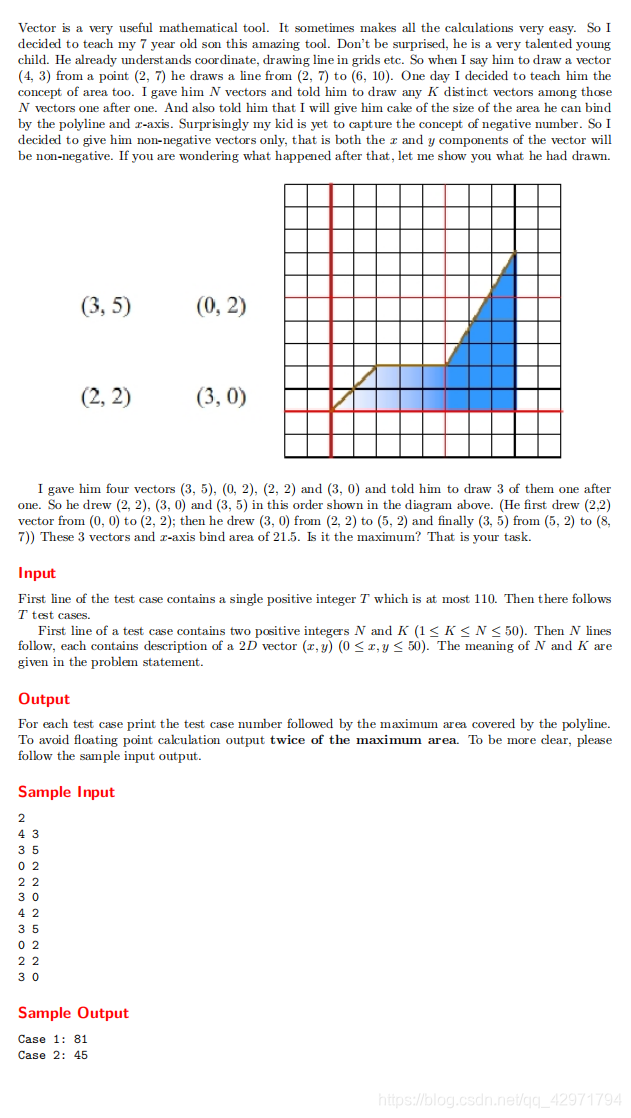
首先，我们将所有向量按斜率从大到小排序。因为在连上某个向量时，在他之前的向量都会为它贡献底部的面积。观察题目的图，可以发现除了第一个向量之外，剩下向量新增的面积都是由底部一个矩形和上面一个三角性组成，而三角形只和当前向量有关，当矩形面积等于当前的总高度乘当前向量的长。因此，向量放的越早，其为后续贡献的矩形面积就越多，因此选择先放斜率大的。
定义：
$dp[i][j][k]$为考虑前$i$个向量，并选择了其中的$j$个并且此时高度为$k$时的最大面积。（$dp$找状态参数可以观察题目，只要一个状态能唯一表示即可）。$DP(ID,Choose,High)$返回考虑到第$ID$个向量，选择了$Choose$个向量，当前高度为$High$作为起始条件后能达到的最大面积。
初始化：
$dp=-1$用-1来标记未搜索过
转移方程及边界条件：

int DP(int ID, int Choose, int High) {
	int& Ans = dp[ID][Choose][High];
	//如果选够了K个，就不能在选了，那以此作为起始条件一个都选不到。
	if (Choose == K) {
		return Ans = 0;
	}
	//枚举到最后一个就返回负无穷（不影响max的结果）
	else if (ID == N) {
		return Ans = -inf;
	}
	//搜索过了就直接返回
	if (~Ans) {
		return Ans;
	}
	Ans = max(
		//不选择第ID个点
		DP(ID + 1, Choose, High),
		//选择第ID个点，答案记得翻倍
		DP(ID + 1, Choose + 1, High + Vector[ID].y) + 2 * Vector[ID].x * High + Vector[ID].x * Vector[ID].y
	);
	//可能会双-inf，啥都选不了，就返回0
	return Ans = max(0, Ans);
}

AC代码：

#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
constexpr static int inf = 0x3f3f3f3f;
struct Node{
	int x, y;
	bool operator<(const Node& Right)const {
		return this->y * Right.x > Right.y * this->x;
	}
}Vector[51];
int N, K;
int dp[51][51][2501];
void Input() {
	cin >> N >> K;
	for (int i = 0; i < N; ++i) {
		cin >> Vector[i].x >> Vector[i].y;
	}
	return;
}
int DP(int ID, int Choose, int High) {
	int& Ans = dp[ID][Choose][High];
	if (Choose == K) {
		return Ans = 0;
	}
	else if (ID == N) {
		return Ans = -inf;
	}
	if (~Ans) {
		return Ans;
	}
	Ans = max(
		DP(ID + 1, Choose, High),
		DP(ID + 1, Choose + 1, High + Vector[ID].y) + 2 * Vector[ID].x * High + Vector[ID].x * Vector[ID].y
	);
	return Ans = max(0, Ans);
}
int main() {
	int T;
	cin >> T;
	for (int Case = 1; Case <= T; ++Case) {
		memset(dp, -1, sizeof(dp));
		Input();
		sort(Vector, Vector + N);
		printf("Case %d: %d\n", Case, DP(0, 0, 0));
	}
	return 0;
}

第$ID$位枚举的都是$ID+1$，也许可以滚动数组优化？懒得想了