@[toc]

堆的简介

转载链接（堆的基本概念）

对顶堆

简介

对顶堆是由一个大顶堆和一个小顶堆组合而成的数据结构，与传统堆维护最大数不同，对顶堆用于动态维护第$k$大的数。在对顶堆中，小根堆位于大根堆的上方，即保证了小根堆的所有数始终比大根堆大。比如维护这样一个数组$[1,4,6,8,10,14,16,18,23,55]$，此时需要维护第7大的数（也就是8），那么此时对顶堆的结构如下图所示。其中，红色的节点为小根堆，绿色的节点为大根堆。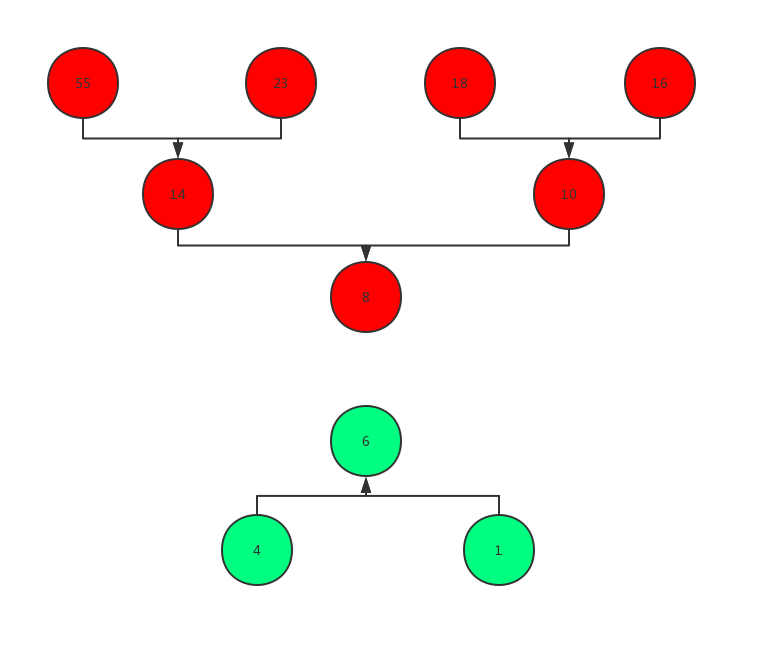对顶堆示意图，作者，OrzzrOOrzzrO
其中，数字8为小根堆对顶，数字6为大根堆堆顶。可以看到，由于小根堆堆底元素小于堆顶，而大根堆堆底元素小于堆顶，这样的组合保证了整个数据结构中上方的元素永远大于下方的。即小根堆的堆顶永远大于大根堆的堆顶。而此时，小根堆的元素有7个，而大根堆的元素有3个，由于小根堆大于大根堆，并且小根堆堆顶元素为小根堆最小的元素，因此所求的第7大的元素即为小根堆的堆顶元8。

$k$值修改

为了保证$k$值在修改后仍能保持这样特殊的数据结构，我们需要在k值发生变化时交换两个堆中的元素，不过每次交换只对相应的堆顶进行操作。比如原先的k值是7，现在将$k$修改为6，那相应的就需要小根堆中的元素数量为6以使得小根堆堆顶元素即为第6大的数。那么需要的操作就是将小根堆的堆顶元素8取出，并将其放入大根堆，此时小根堆中的元素数量为6，而大根堆的元素数量为4，这样此时小根堆堆顶元素即为第k大的数（第6大）。此时的对顶堆结构如下图所示。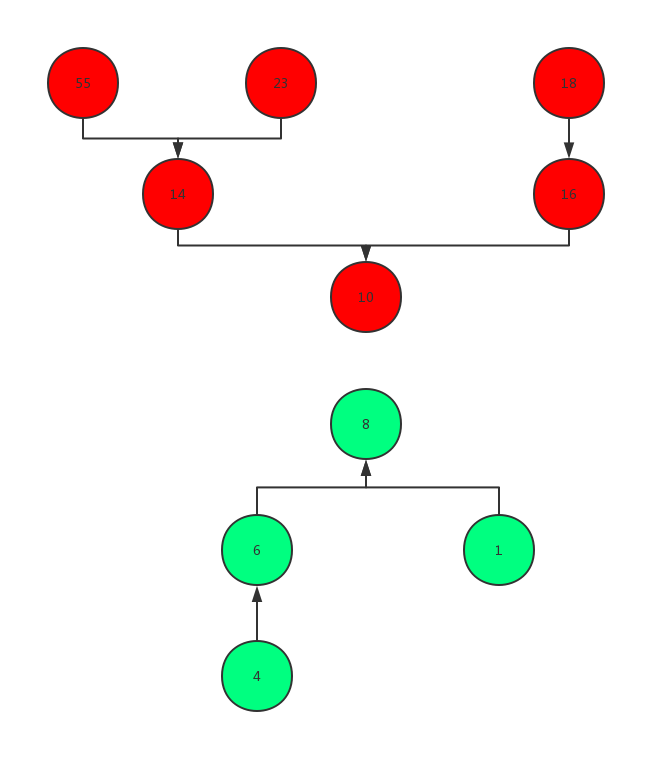
对顶堆示意图，作者，OrzzrOOrzzrO
同理，当$k$值递增时，只需要将小根堆堆顶元素取出，并将其放入大根堆中即可。对于k值的每次修改，假设当前堆中有共有$N$个元素，即小根堆中有$k$个元素，大根堆中有$N-k$个元素，即$k$的每次递增或递减的时间复杂度为$O(logk+log(N-k))=O(log(Nk-k^2))$。而普通的二叉平衡树在查询第$k$大的数（对二叉平衡树进行中序遍历）的时间复杂度为$O(k)$。

插入和删除

对顶堆的元素插入只要将元素插入大根堆即可，时间复杂度$O(log(N-k))$。
对顶堆的元素删除，首先将待删除元素和两个堆的堆顶比较以确定元素在哪个堆中，如果在大根堆中，则直接删除，时间复杂度为$O(logN-k)$，如果在小根堆中，则将元素删除后为了维护小根堆大小，即$k$值，需要将大根堆的堆顶元素移到小根堆中，时间复杂度为$O(log(N-k)+log(k))$。而有序数组虽然能做到$O(1)$查询，修改的时间复杂度却达到了$O(N^2)$。

总结

即对于在线查询第k大的数以及需要支持修改时，若k时呈递增递减、单次变化很小或不变时，对顶堆是更好的选择。当然，如果k的值波动较大，就不适合使用对顶堆了。将问题简化一下，设每次$k$的变化值为$x$，即当$xlogN \leq N$时,对顶堆的表现会更好，否则应采用普通的平衡树或堆。

例题

洛谷P1801

题目描述
Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。
命令只有两种：
ADD(x):把x元素放进BlackBox;
GET:i加1，然后输出Blackhox中第i小的数。
记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：
我们来演示一下一个有11个命令的命令串。（如下图所示）
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：
1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。
2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。
输入格式
第一行，两个整数，M，N。
第二行，M个整数，表示A(l)……A(M)。
第三行，N个整数，表示u(l)…u(N)。
输出格式
输出Black Box根据命令串所得出的输出串，一个数字一行。
输入输出样例
输入
7 4
3 1 -4 2 8 -1000 2
1 2 6 6
输出
3
3
1
2
说明/提示 对于30%的数据，M≤10000;
对于50%的数据，M≤100000：
对于100%的数据，M≤200000。

这里采用了std::set来模拟堆操作（实际上手写堆或std::priority_queue会更快）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#include<algorithm>
#include<set>
using namespace std;
int a[200001],
	b[200001],
	m,
	n;
multiset<int>minHeap;
multiset<int, greater<int>>maxHeap;
inline void input() {
	scanf("%d%d", &m, &n);
	for (int i = 1; i <= m; ++i) {
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= n; ++i) {
		scanf("%d", &b[i]);
	}
}
inline void work() {
	int cur = 1;
	for (int i = 1; i <= n; ++i) {
		for (; cur <= b[i]; ++cur) {
			maxHeap.insert(a[cur]);
			if (maxHeap.size() == i) {
				minHeap.insert(*maxHeap.begin());
				maxHeap.erase(maxHeap.begin());
			}
		}
		printf("%d\n", *minHeap.begin());
		maxHeap.insert(*minHeap.begin());
		minHeap.erase(minHeap.begin());
	}
}

int main() {
	input();
	work();
}

例题二 操作系统

洛谷P2278

题目描述
写一个程序来模拟操作系统的进程调度。假设该系统只有一个CPU，每一个进程的到达时间，执行时间和运行优先级都是已知的。其中运行优先级用自然数表示，数字越大，则优先级越高。
如果一个进程到达的时候CPU是空闲的，则它会一直占用CPU直到该进程结束。除非在这个过程中，有一个比它优先级高的进程要运行。在这种情况下，这个新的（优先级更高的）进程会占用CPU，而老的只有等待。
如果一个进程到达时，CPU正在处理一个比它优先级高或优先级相同的进程，则这个（新到达的）进程必须等待。
一旦CPU空闲，如果此时有进程在等待，则选择优先级最高的先运行。如果有多个优先级最高的进程，则选择到达时间最早的。
输入格式
输入包含若干行，每一行有四个自然数（均不超过$10^8$），分别是进程号，到达时间，执行时间和优先级。不同进程有不同的编号，不会有两个相同优先级的进程同时到达。输入数据已经按到达时间从小到大排序。输入数据保证在任何时候，等待队列中的进程不超过15000个。
输出格式
按照进程结束的时间输出每个进程的进程号和结束时间。
输入输出样例
输入
1 1 5 3
2 10 5 1
3 12 7 2
4 20 2 3
5 21 9 4
6 22 2 4
7 23 5 2
8 24 2 4
输出
1 6
3 19
5 30
6 32
8 34
4 35
7 40
2 42

一道模拟加堆优化的题目。每当读入一个进程时，如果该进程的到来时间晚于已存在队列中进程执行完的时间，就先将队列头的进程执行完在将读入的进程加入队列，否则就直接将读入进程加入队列。可以考虑使用优先队列来维护进程顺序，降低时间复杂度，比较函数定义为进程优先级的大小比较，在优先级相等时考虑时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<iostream>
#include<algorithm>
#include<set>
#include<queue>
using namespace std;

struct Process {
	int node,//编号
		start,//开始时间
		length,//持续时间
		priority;//优先级
	Process(int&n,int&s,int&l,int&p):node(n),start(s),length(l),priority(p) {
	}
	Process() = default;
	bool operator<(const Process&Right)const {//定义比较函数
		if (this->priority == Right.priority) {
			return this->start > Right.start;
		}
		else {
			return this->priority < Right.priority;
		}
	}
};

priority_queue<Process> Q;

int main() {
	Process CurrentProcess;
	int time;//当前时间
	int n, s, l, p;
	scanf("%d%d%d%d", &n, &s, &l, &p);
	Q.push(Process(n, s, l, p));
	time = Q.top().start;//为第一个到达进程的到达时间
	while (scanf("%d%d%d%d", &n, &s, &l, &p) != EOF) {
		Process next(n, s, l, p);
		time = max(time, Q.top().start);//当前时间更新
		//如果读入进程晚于当前进程执行完时间就先执行，否则加入队列。
		while (!Q.empty()&&Q.top().length + time <= next.start) {
			CurrentProcess = Q.top();
			Q.pop();
			time += CurrentProcess.length;
			printf("%d %d\n", CurrentProcess.node, time);
			if (!Q.empty()) {
				time = max(time, Q.top().start);
			}
		}
		//如果新加入进程优先级大于队列顶进程
		if (!Q.empty()&&Q.top() < next) {
			CurrentProcess = Q.top();
			Q.pop();
			//队列顶进程可以先执行（当前时间到下一进程的空白时间）
			CurrentProcess.length -= next.start - time;
			Q.push(CurrentProcess);
		}
		Q.push(next);
	}
	//清空队列
	while (!Q.empty()) {
		CurrentProcess = Q.top();
		Q.pop();
		time = CurrentProcess.length + (time > CurrentProcess.start ? time : CurrentProcess.start);
		printf("%d %d\n", CurrentProcess.node, time);
	}
}

例题三 序列合并

洛谷P1631

题目描述
有两个长度都是N的序列A和B，在A和B中各取一个数相加可以得到$N^2$个和中最小的$N$个。
输入格式
第一行一个正整数$N$；
第二行$N$个整数$A_i$, 满足$A_i​≤10^9$;
第三行$N$个整数$B_i$,满足$B_i​$≤$10^9$.
【数据规模】
对于50%的数据中，满足$1\leq N\leq 1000$；
对于100%的数据中，满足$1\leq 100000$。
输出格式
输出仅一行，包含N个整数，从小到大输出这N个最小的和，相邻数字之间用空格隔开。
输入输出样例
输入
3
2 6 6
1 4 8
输出
3 6 7

首先暴力的方法就是将这$N^2$个和都求出来，然后进行排序，但是显然这样做的时间复杂度会高达$O(N^{2}logN)$，对于100000显然不得行。但是发现给出数据是排好序的，显然我们可以先把$a$中最小的$a[0]$和$b$先加起来得到$N$个和，接着在$a[1]$和$b$相加时，因为$a[1]\geq a[0]$，所以当$i$达到一定值后，必然会出现$a[1]+b[i]\geq a[0]+b[n-1]$(最大的b值)，那这时，就没必要往下找了，就接着找$a[2]$了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<algorithm>
#include<set>
#include<queue>
using namespace std;
int a[100001], b[100001], N;
//采用优先队列维护n个最小和
priority_queue<int>Q;
inline void input() {
	scanf("%d", &N);
	for (int i = 1; i <= N; ++i) {
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= N; ++i) {
		scanf("%d", &b[i]);
	}
}
int main() {
	input();
	//先将a[1]和b加起来得到n个和
	for (int i = 1; i <= N; ++i) {
		Q.push(a[1] + b[i]);
	}
	//全排列枚举
	for (int i = 2; i <= N; ++i) {
		for (int j = 1; j <= N; ++j) {
			int&&sum = a[i] + b[j];
			//当当前和比队列中最大值还大时就没必要往下找了
			if (Q.top() <= sum) {
				break;
			}
			Q.pop();
			Q.push(sum);
		}
	}
	//从小到达输出
	for (int i = 1; i <= N; ++i) {
		a[i] = Q.top();
		Q.pop();
	}
	for (int i = N; i >= 1; --i) {
		printf("%d ", a[i]);
	}
}

关于时间复杂度，a[0]插入了$N$个元素，a[1]最多扫描前$\frac{2}{N}$,一直到a[n-1]最多扫描前1个元素，而优先队列的插入删除时间复杂度为$O(logN)$，所以总体时间复杂度为$O(NlogN(1+\frac{1}{2} + \frac{1}{3}+\cdots + \frac{1}{N}) = O(NlogNlnN)=O(Nlog^{2}N)$。

例题四 最小函数值

洛谷P2085

题目描述 有n个函数，分别为$F_1,F_2,\cdots,F_n$。定义$F_i(x)=A_ix^2+B_ix+C_i (x∈N^+)$。给定这些$A_i、B_i$和$C_i$，请求出所有函数的所有函数值中最小的m个（如有重复的要输出多个）。
输入格式 输入数据：第一行输入两个正整数n和m。以下n行每行三个正整数，其中第i行的三个数分别为$A_i、B_i$和$C_i$。$A_i\leq10，B_i\leq100，C_i\leq10000$。
输出格式
输出数据：输出将这n个函数所有可以生成的函数值排序后的前m个元素。这m个数应该输出到一行，用空格隔开。
输入输出样例
输入
3 10
4 5 3
3 4 5
1 7 1
输出
9 12 12 19 25 29 31 44 45 54
说明/提示 数据规模：n,m<=10000

和例题三的思路是完全一样的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<iostream>
#include<algorithm>
#include<set>
#include<queue>
#include<vector>
using namespace std;
struct Fun{
	int A, B, C;
	Fun(int&a, int&b, int&c) :A(a), B(b), C(c) {  }
	int get(int&val) {
		return A * val*val + B * val + C;
	}
};
vector<Fun> funs;
priority_queue<int>Q;
vector<int> ans;
int m, n;
inline void input() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i) {
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		funs.push_back(Fun(a, b, c));
	}
}
inline void init() {
	for (int i = 1; i <= m; ++i) {
		Q.push(funs[0].get(i));
	}
}
inline void compute() {
	for (int i = 1; i < funs.size(); ++i) {
		int cnt = 0;
		while (true) {
			int &&val = funs[i].get(++cnt);
			if (Q.top() <= val) {
				break;
			}
			else {
				Q.pop();
				Q.push(val);
			}
		}
	}
}
inline void reserve() {
	while (!Q.empty()) {
		ans.push_back(Q.top());
		Q.pop();
	}
}
inline void output() {
	for (auto it = ans.crbegin(); it != ans.crend(); ++it) {
		printf("%d ", *it);
	}
}
int main() {
	input();
	init();
	compute();
	reserve();
	output();
}

例题五 种树

洛谷P1484

题目描述
cyrcyr今天在种树，他在一条直线上挖了n个坑。这n个坑都可以种树，但为了保证每一棵树都有充足的养料，cyrcyr不会在相邻的两个坑中种树。而且由于cyrcyr的树种不够，他至多会种k棵树。假设cyrcyr有某种神能力，能预知自己在某个坑种树的获利会是多少（可能为负），请你帮助他计算出他的最大获利。
输入格式
第一行，两个正整数n,k。
第二行，n个正整数，第i个数表示在直线上从左往右数第i个坑种树的获利。
输出格式
输出1个数，表示cyrcyr种树的最大获利。
输入输出样例
输入
6 3
100 1 -1 100 1 -1
输出
200
说明/提示 对于20%的数据，n<=20。
对于50%的数据，n<=6000。
对于100%的数据，n<=500000，k<=n/2,在一个地方种树获利的绝对值在1000000以内。

$O(n^2)$做法：

动态规划，定义$dp[i][j]$为种到第i棵树时种第j棵树的最大收益，那么状态转移方程为$dp[i][j]=max(dp[i-1][j],dp[i-2][j-1]+a[j])$，$a[j]$为第j棵树的收益。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#include<algorithm>
#include<set>
#include<queue>
#include<cmath>
#include<vector>
using namespace std;
int n, k;
int a[500001];
int dp[4][500001];
constexpr int mod = 3;
inline void input() {
	scanf("%d%d", &n, &k);
	for (int i = 1; i <= n; ++i) {
		scanf("%d", &a[i]);
	}
}
inline void DP() {
	dp[1][1] = max(0, a[1]);
	dp[2][1] = max(a[1], max(0, a[2]));
	for (int i = 3; i <= n; ++i) {
		//最多种 n/2棵树
		for (int j = 1; j <= ceil(double(i)/2.); ++j) {
			dp[i%mod][j] = max(dp[(i - 1)%mod][j], dp[(i - 2)%mod][j - 1] + a[i]);
		}
	}
}
inline void output() {
	int ans = dp[n%mod][1];
	for (int i = 2; i <= k; ++i) {
		ans = max(dp[n%mod][i], ans);
	}
	printf("%d\n", ans);
}
int main() {
	input();
	DP();
	output();
}

$O(klogn)$做法：

我们发现，当第$i$棵树被种下时，第$i+1$和$i+1$棵树就不能被种了。所以对于第$i+1$和$i-1$棵树，有三种情况：只有一棵树被种，没有树被种以及两棵树都被种。可以发现，对于只有一颗树被种时（$i+1$或$i-1$），第i棵树肯定不能种，那就等价于第$i+1$或$i-1$棵树单独被种的情况，也就是第i以及第i+2棵树不被中或第i-2棵树以及第i棵树不被中，那么此时只有一棵树被种的情况相当于考虑其相邻树时的情况。
因此，需要考虑的情况为第i棵树同时被种或同时不被种的情况。
首先，使用双向链表来标记所有树洞的位置，一开始左右相邻，当选择第$i-1$和$i+1$个树洞种树时，第$i$个树不种，这是可以考虑将$i-1，i，i+1$这三个树洞合并为一个树洞，并且这个新的树洞增加的收益为$a[i+1]+a[i-1]-a[i]$，如此相较于种第i棵树多种了一棵树，如此循环直到种满$n$棵树即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<iostream>
#include<algorithm>
#include<set>
#include<queue>
#include<vector>
using namespace std;
long long n, k;
long long a[500001];//树洞收益
long long Left[500001],Right[500001];//双向链表
bool isDelete[500001]{ false };//标记已被合并的树洞，避免重复选择。
struct Node {
	int node;
	long long val;
	Node(int&node, long long&val):node(node), val(val) {  }
	bool operator<(const Node&Right)const {
		return this->val < Right.val;
	}
};
priority_queue<Node> Q;//优先队列
inlicne void input() {
	scanf("%lld%lld", &n, &k);
	for (int i = 1; i <= n; ++i) {
		scanf("%lld", &a[i]);
		Q.emplace(i, a[i]);
	}
}
//初始化双向链表
inline void init() {
	for (int i = 1; i <= n; ++i) {
		Left[i] = i - 1;
		Right[i] = i + 1;
	}
}
long long compute() {
	long long ans = 0;//总收益
	while (k--) {//循环执行k次，表示最多种k棵树
		//当队头已经被合并了就不要
		while (isDelete[Q.top().node]) {
			Q.pop();
		}
		auto N = Q.top();
		Q.pop();
		//当前待处理树洞中的最大收益小于0时就没必要再种了
		if (N.val < 0) {
			break;
		}
		//种下这棵树
		ans += N.val;
		int&node = N.node;
		//将node+1，node，node-1合并为node
		a[node] = a[Left[node]] + a[Right[node]] - a[node];
		isDelete[Left[node]]=isDelete[Right[node]]=true;
		//链表合并
		Left[node] = Left[Left[node]];
		Right[Left[node]] = node;
		Right[node] = Right[Right[node]];
		Left[Right[node]] = node;
		//入队
		Q.emplace(node, a[node]);
	}
	return ans;
}
int main() {
	input();
	init();
	printf("%lld\n", compute());
}